Chapter 8 – Several Variables and Partial Derivatives
8.1 Vector spaces, linear mappings, and convexity
Note: 2–3 lectures
8.1.1 Vector spaces
The euclidean space![]() has already made an appearance in the metric space chapter. In this chapter, we extend the differential calculus we created for one variable to several variables. The key idea in differential calculus is to approximate differentiable functions by linear functions (approximating the graph by a straight line). In several variables, we must introduce a little bit of linear algebra before we can move on. We start with vector spaces and linear mappings on vector spaces.
has already made an appearance in the metric space chapter. In this chapter, we extend the differential calculus we created for one variable to several variables. The key idea in differential calculus is to approximate differentiable functions by linear functions (approximating the graph by a straight line). In several variables, we must introduce a little bit of linear algebra before we can move on. We start with vector spaces and linear mappings on vector spaces.
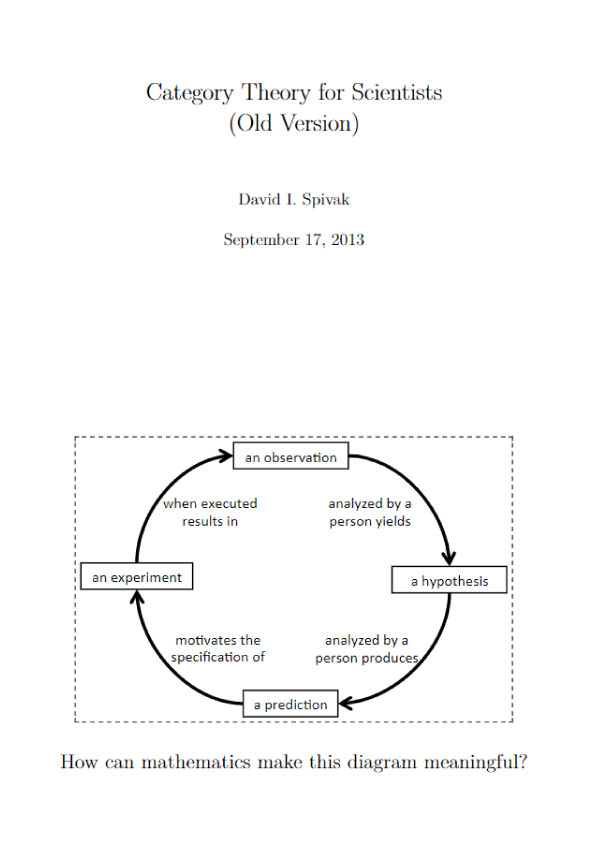
While it is common to use![]() or the bold v for elements of Rn, especially in the applied sciences, we use just plain old v, which is common in mathematics. That is, v ∈ Rn is a vector, which means v = (v1,v2, . . . ,vn) is an n-tuple of real numbers. * It is common to write and treat vectors as column vectors, that is, n-by-1 matrices:
or the bold v for elements of Rn, especially in the applied sciences, we use just plain old v, which is common in mathematics. That is, v ∈ Rn is a vector, which means v = (v1,v2, . . . ,vn) is an n-tuple of real numbers. * It is common to write and treat vectors as column vectors, that is, n-by-1 matrices:
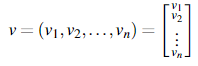
We will do so when convenient. We call real numbers scalars to distinguish them from vectors.
We often think of vectors as a direction and a magnitude and draw the vector as an arrow. The vector (v1,v2, . . . ,vn) is represented by an arrow from the origin to the point (v1,v2, . . . ,vn), see Figure 8.1 in the plane R2. When we think of vectors as arrows, they are not based at the origin necessarily; a vector is simply the direction and the magnitude, and it does not know where it starts.
On the other hand, each vector also represents a point in Rn. Usually, we think of v ∈ Rn as a point if we are thinking of Rn as a metric space, and we think of it as an arrow if we think of the so-called vector space structure on Rn (addition and scalar multiplication). Let us define the abstract notion of a vector space, as there are many other vector spaces than just Rn.
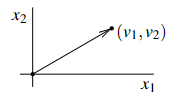
Figure 8.1: Vector as an arrow.
Definition 8.1.1. Let X be a set together with the operations of addition, + : X ×X → X , and multiplication, · : R×X → X , (we usually write ax instead of a · x). X is called a vector space (or a real vector space) if the following conditions are satisfied:
(i) (Addition is associative) If u,v,w ∈ X , then u+(v+w) = (u+ v)+w.
(ii) (Addition is commutative) If u,v ∈ X , then u+ v = v+u.
(iii) (Additive identity) There is a 0 ∈ X such that v+0 = v for all v ∈ X .
(iv) (Additive inverse) For every v ∈ X , there is a −v ∈ X , such that v+(−v) = 0.
(v) (Distributive law) If a ∈ R, u,v ∈ X , then a(u+ v) = au+av.
(vi) (Distributive law) If a,b ∈ R, v ∈ X , then (a+b)v = av+bv.
(vii) (Multiplication is associative) If a,b ∈ R, v ∈ X , then (ab)v = a(bv).
(viii) (Multiplicative identity) 1v = v for all v ∈ X .
Elements of a vector space are usually called vectors, even if they are not elements of Rn (vectors in the “traditional” sense).
If Y ⊂ X is a subset that is a vector space itself using the same operations, then Y is called a subspace or a vector subspace of X .